Measurement of Cellular Contractile Forces Using Patterned Elastomer
1. INTRODUCTIONThe adhesive interaction of cells with their neighbors and with the extracellular matrix is a characteristic feature of all metazoan organisms. Cell adhesion is essential for cell migration, tissue assembly, and the direct communication of cells with their immediate environment. These interactions are mediated via specific cell surface receptors that specifically interact with the external surface, and link it, across the membrane, with the actin cytoskeleton (Geiger et al., 2001). These multimolecular complexes are subjected to constant mechanical perturbation, generated either by the cellular contractile system or by changes in the neighborhood of the cell. To list just a few examples, in the course of cell migration, focal adhesions (FA) are formed, where contractile microfilament bundles, consisting of actin and myosin, are anchored. Their pulling on the substrate is involved in regulating the adhesion itself, as well as in coordinating the persistent forward movement of the cell. Mechanical perturbations are generated by diverse external factors, such as muscle contraction, blood flow, gravitational forces, and acoustic waves. Both internal and external forces apparently act at adhesion sites and modulate their organization and signaling activity (Geiger and Bershadsky, 2001; Riveline et al., 2001; Galbraith et al., 2002). In view of the major physiological significance of these cellular forces, it appears important to develop approaches for the accurate measurement of cellular forces with an appropriate sensitivity and spatial resolution (Beningo and Wang, 2002; Roy et al., 2002). This article describes an approach for measuring such forces using the patterned polydimethylsiloxane (PDMS) elastomer as an adhesive substrate and cells expressing fluorescent focal adhesion molecules (Balaban et al., 2001). These experiments demonstrated that cells maintain a constant stress at focal adhesion sites, of the order of ~5nN/µm2, and that changes in cellular contractility lead rapidly to changes in FA organization. This article describes the technique used for the preparation of the patterned elastomeric substrate and for measuring the cellular forces.
II. MATERIALS AND EXPERIMENTATION
A. Lithography
Silicone wafer
Photoresist: Microposit S1805 (Shipley, Marlborough, MA)
Developer: Microposit MF-319 (Shipley)
HMDS or tridecafluorooctyltrichlorosilane (UCT, Bristol, PA)
Acetone, methanol
Spinner (Headway Research, Inc., Garland TX)
Mask aligner (Karl Suss, MJB3, Germany)
Chrome mask with desired pattern, or transparency
Digital hot plates
Oven
Scriber
B. Elastomer
PDMS: Sylgard 184, Dow Corning
No. 1 glass coverslips (diameter 25 mm)
Oven
C. Microscopy
The DeltaVision microscopy system (Applied Precision Inc., Issaquah, WA) is used in these experiments. Similar microscopy systems could be used for such purpose, provided that they are capable of accurately acquiring high-resolution images (512 × 512 pixels or better) at a high sensitivity (allowing for lowdose recording) and high dynamic range (12 bit or better).
D. Calibration
Bulk calibration: weights, clamps
Calibrated micropipettes with elastic constants 10- 50 nN µm-1
E. Image Analysis
Image analysis software: Priism (Applied Precision Inc.)
Data analysis software: Matlab (The Mathworks, Natick, MA) (This software can be purchase with image analysis toolbox and used to perform the image analysis as well)
F. Calculation of Forces
A detailed description of this calculation is provided in a web site established by Dr. Ulrich Schwartz (see later).
III. PROCEDURES
A. Lithography
This step provides molds consisting of a pattern of photoresist on silicon wafer that will be used for the patterning of elastomer substrates, a technique termed "soft lithography" (Whitesides et al., 2001). It relies on access to a clean room with basic optical lithography. It also assumes the availability of the chrome mask with the pattern of interest. For high-resolution patterns (features below 1 µm), such masks are produced by electron beam lithography (also available in many clean room facilities). For low-resolution patterns (5µm features and more), transparencies with appropriate resolution (5080dpi) can be used.
- Clean silicon wafer in acetone and then immediately wash with methanol and blow dry.
- (Optional) Bake for 20min in a 120°C oven.
- Dispense HMDS in the middle of the wafer until full coverage and spin at 6000rpm for 1 min.
- Dispense S1805 photoresist in the middle of the wafer covering approximately one-third of the wafer and spin at 5000rpm for 30s.
- Soft bake on hot plate at 80°C for 5 min.
- Make sure the wafer and the mask are in contact in the mask aligner.
- Expose for 10s. This number is only an estimate; exposure and development times have to be adjusted for the specific exposure system. Typically an exposure of 100-140 mJ/cm2 is recommended.
- Develop for 10s (see aforementioned comment).
- Hard bake for 5 min in a 120°C oven.
- In order to prevent sticking between the mold and the PDMS, an additional spin of HMDS can be performed at this stage. Alternatively, overnight exposure to vapors of tridecafluorooctyltrichlorosilane can be done.
- Dice the wafer with a scriber in small pieces of about 5 × 5 mm. Each of these pieces can be reused as a mold many times for patterning of the PDMS substrates.
B. Elastomer Substrates
- Pour about 30 ml of part A of the Sylgard 184 kit. Add 1 part of B (cross-linker) for 50 parts of A (in weight): Mix thoroughly.
- Cover and let stand on bench until bubbles are scarce (typically 30min).
- Coat glass coverslips with the PDMS mixture. For large patterns that can be seen with low-resolution, long working distance objectives, put a few drops of the mixture in the middle of the coverslip on a flat surface covered with aluminium foil and let flow until the whole coverslip is covered. For short working distance objectives, a thinner layer is needed. This can be achieved by spinning No.1 coverslips at 1000rpm on a spinner equipped with a 0.05-in. rotating head or "chuck." Alternatively, coverslips coated with PDMS can be put vertically to allow the flow of excess PDMS and attain a thinner thickness (typically 0.05mm).
- Place the coated coverslips on aluminium foil and bake in an oven at 65°C for 25 min until the top layer of the PDMS has started to solidify.
- Place the rest of the PDMS mixture in the oven for bulk calibration purposes (see Section III,D).
- Place a piece of the mold in the center of each coverslip (the patterned side of the mold should be in contact with the PDMS) and put back in oven overnight.
- Delicately separate the mold from the patterned coverslip.
- Glue each patterned coverslip to the botton of a 35-mm tissue culture plate with a 15-mm hole. This step can be done with melted paraffin.
- Wash the coverslip and dish extensively with phosphate-buffered saline (PBS).
- Incubate at 4°C overnight with a solution of 10µg/ml of fibronectin in PBS.
- Before plating the cells, wash the fibronectin solution with fresh plating medium twice and incubate the substrates with medium at 37°C for 1h.
- Plate cells at appropriate dilution and incubate immediately until observation.
C. Microscopy
Images are recorded, using phase-contrast or fluorescence optical mode, with a DeltaVision system digital microscopy system. This system is based on a Zeiss inverted microscope equipped with filter sets for multiple color microscopy and a high-resolution, scientific- grade CCD camera. Images are acquired using high numerical aperture oil objectives for the highresolution pattern and focal adhesion detection (Fig. 3); long distance objectives are used for semiquantitative estimates of force using large patterns (Fig. 2). Image processing is conducted primarily using the Prism software of the DeltaVision system.
D. Calibration of Elastic Properties of the Elastomer
The aim of this step is to determine whether the cured PDMS is an elastomer and to obtain the two parameters that characterize its elasticity, namely the Young modulus (Y) and the Poisson ratio (σ) (Feynman, 1964).
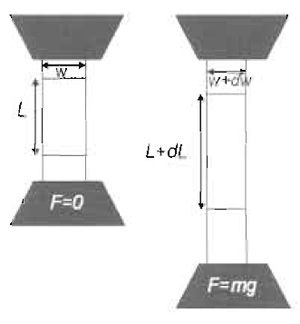 |
| FIGURE 1 Bulk calibration of the elastomer. A stripe of PDMS prepared in parallel to preparation of elastomer substrates is checked for its elastic properties. The procedure consists of subjecting the stripe to increasing masses while measuring the force-extension response. |
1. Bulk Calibration
Cut strips of cured elastomer (see Section III,B, step 5). Typically a strip of 100 × 30 × 5 mm can be used. Hold each side with clamps wider than the strip. With a marker, draw two lines on the elastomer, away from the clips, separated by about 50mm. The distance between the lines is marked as L in Fig. 1. Add increasing masses, m, to the lower clamp and measure the total increase in length, dL, until dl > L. Plot the relation
| dl | (m) |
| L |
with m expressed in kilograms. Verify that the relation is linear and extract the linear coefficient, α. The Young modulus
(in Pa) is given by
| Y= | g |
| Aα |
with A = w*h, the cross section of the strip (in m2), and
g = 9.8ms-2.
| dw | = | dh | = | -σ | dl |
| w | h | L |
The strips should be stretched overnight to verify that they relax to their original length, L, once the weights are removed.
2. In Situ Calibration
In order to verify that the plating of cells does not modify the elastic characteristics of the surface, in situ calibration of the elasticity of the patterned substrate is performed under a microscope.
Mount the calibrated micropipette on a micromanipulator. Approach the surface slowly, keeping the micropipette parallel to the patterned elastomer surface. Once the tip of the micropipette is in contact with the surface, acquire an image of the patterned elastomer and of the tip of the pipette. Slowly move the stage by 2-3 µm in order to create a stress between the micropipette and the surface. Acquire a new image of the deformed pattern and of the micropipette bending. Usually, images at different magnifications are necessary in order to visualize the distortions of the pattern and of the micropipette. The force exerted by the micropipette is measured directly by quantifying the deflection of the pipette in the image. Verify that the calculation of force using the bulk Young modulus agrees with the known force exerted by the calibrated micropipette.
 |
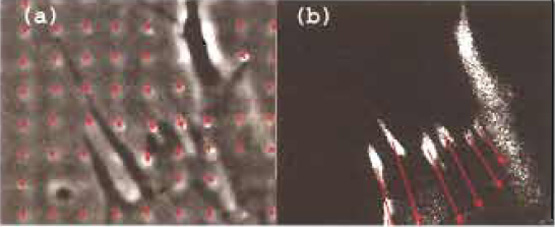
| FIGURE 2 Rapid semiquantitative estimate of forces (Balaban et al., 2001). A large grid-patterned elastomer is used for the easy visualization of distortions. (a) A rat cardiac fibroblast exerts forces on the elastomer substrates, which result in deformations of the grid (marked by arrows). (b) Once the forces are relaxed by adding an inhibitor of contractility, the grid returns to its original regular shape. Grid size: 30 µm. |
 |
| FIGURE 3 From displacements to forces (Balaban et al., 2001).
(a) Phase-contrast image of a small part of a fibroblast on the highresolution
dot pattern. Arrows denote displacements of the center
of mass of the dots relative to the relaxed image. Pitch size: 2µm.
(b) Fluorescence image of the same field of view showing locations
of the focal adhesions. The length of the arrows here indicates the
forces at each focal adhesion, calculated from displacement data. |
E. Image Analysis
Substrates with low resolution patterns such as the 30-µm grid shown in Fig. 2 can provide semiquantitative estimates of the mechanical perturbation due to cells and is useful for the rapid comparison between different cell types or conditions. However, for the quantitative measurement of the forces at single adhesion sites, high-resolution patterns of dots (Fig. 3a), as well as fluorescence tagging of adhesion sites, are needed (Fig. 3b). In this section, it is assumed that the following images are available for the same field of view.
- Phase contrast of cells on a high-resolution pattern of dots ("dot_force.tif").
- Phase contrast of the high-resolution pattern of dots, after forces have been relaxed ("dot_relaxed.tif"), namely after treatment with acto-myosin inhibitors or trypsinization. Alternatively, locations of the dots in the relaxed pattern can be generated directly as ("center_relaxed.dat") by assuming the regularity of the pattern.
- Fluorescence image of adhesion sites ("focals.tif").
Registration of Images
In order to correct for eventual shifts during image acquisitions, all three images should be aligned using fixed reference points. Typically, corrections of a few pixels shift in x or y might be needed; angular shift are infrequent.
The step is performed using the registration option of the image analysis software.
Detection of the Pattern
This step automatically detects the dots in the two phase-contrast images and outputs their center-ofmass coordinates to an ASCII file. It is important to use the same parameters for both images.
- Filter "dot force.tif " and dot relaxed.tif" with a large kernel in order to correct for background unevenness.
- Depending on the image quality, use a high pass filter with a small kernel to enhance the dots contrast on both images.
- Perform segmentation for the detection of the dots. Verify that the segmentation detected the dots properly. Correct manually for eventual defects.
- Save the center of mass coordinates of the dots in each picture in two separate ASCII files ("center_relaxed.dat" and "center_force.dat").
- Using Matlab, load the two ASCII files and arrange in pairs nearest neighbors according to their center of mass coordinates to identify equivalent dots between the two files. This will work for most of the image where there are no displacements. In areas where displacements are larger than the distance between dots, manual corrections might be needed (see Section III,F). Save data as an ASCII file ("lines.dat") whose first two columns are the x and y coordinates of the dots in "center relaxed.dat" and the D last two columns are the x and y coordinates of the equivalent dots from "center_force.dat".
- Visualization of the displacements: load "lines.dat" using a procedure for drawing arrows in the image analysis software (DrawArrows in Prism) on top of the phase-contrast images. Correct for wrong or missing arrows. Save corrections.
3. Detection of Focal Adhesions This step automatically detects focal adhesions in the fluorescence image of cells with GFP-tagged focal adhesion protein (Zamir et al., 1999). ("focals.tif") and outputs their center-of-mass coordinates to an ASCII file ("focals.dat"). The segmentation procedure is analogous to the detection of dots in the pattern.
F. Calculation of Forces
The main advantage of flat elastic substrates is that they interfere little with cell adhesion as traditionally studied on glass or plastic surfaces. In particular, by using transparent elastomers such as PDMS, one can use the normal setups for light microscopy. The main disadvantage of flat elastic substrates is that a computational technique has to be implemented to calculate force from displacement. For the procedure described here, a package with Matlab routines can be downloaded from http://www.mpikggolm.mpg.de/th/ people/schwarz/ElasticSubstrates/. For well-spread cells, one can assume that forces are applied to the top side of the elastic film mainly in a tangential fashion. Because the PDMS film is much thicker than typical displacements on its top side, one can moreover assume that displacements follow from forces as in the case of an elastic half-space. Because we focus on forces from single focal adhesions, where force is localized to a small region of space (namely the focal adhesion), we finally assume that each focal adhesion corresponds to one point force. Then displacement follows from force as described by the well-known Boussinesq solution for the Green function (Landau and Lifshitz, 1970). Since we only consider the case of small deformations (i.e., magnitude of strain tensor | uij | < 1), we deal with linear elasticity theory, and deformations resulting from different force centers can be simply added up to give overall deformation at a given point. However, because the Green function of a point force diverges for small distance r as 1/r, we first use the Matlab program "data.m" to clear the file "lines.dat" from all displacement data points, which are closer to the positions of the focal adhesions in "focals.dat" than a distance of the order of the size of focal adhesions [this procedure can be justified with the concept of a force multipolar expansion (Schwarz et al., 2002)]. This gives a new file "newlines.dat", which together with "focals.dat" is used by our main Matlab program, "inverse.m". Since we are interested in force as a function of displacement, but the Boussinesq solution from linear elasticity theory describes deformation as a function of force, we now have to solve an inverse problem. Because the elastic kernel effectively acts as a smoothing operation that removes high-frequency data, this inversion is ill posed in presence of noise in displacement data: small differences in displacement data can result in large differences in the force pattern. Due to the noise problem, we only can estimate force through a χ2 minimization. Moreover, the target function has to be extended by a so-called regularization term, which prevents the program from reproducing every detail of displacement data through a force estimate with unrealistically large forces. Therefore, we add a quadratic term in force to the target function, which guarantees that forces do not become exceedingly large. The regularization procedure introduces an additional variable, the regularization parameter λ, whose value is fixed by the program "inverse.m" with the help of the so-called discrepancy principle, which states that the difference between measured displacement and displacement following from the force estimate should attain a certain nonvanishing value. Because the target function remains quadratic for the simple regularization term used, it can be inverted easily by singular value decomposition. For this purpose, the Matlab program "inverse.m" uses the freely available package of Matlab routines Regularization Tools by P. C. Hansen. Finally the force estimate is saved in a new ASCII file "forces.dat", which for each entry in "focals.dat" gives the corresponding force estimate. Force calibration assumes the value σ = 0.5 for the Poisson ratio and requires values for Young modulus Y and microscope resolution. The resolution of this procedure depends on the details of the force pattern under consideration, but can be estimated by data simulation. Even under the most favorable conditions, which can be achieved experimentally in regard to quality of displacement data, the original force cannot be reproduced completely and regularization is required to arrive at a reasonable estimate. Spatial and force resolutions have been found to be better than 4µm and 4nN, respectively. Therefore the calculated point force should be correlated with other properties of a focal adhesion only when no other focal adhesions are closer than the spatial resolution of our method.
IV. PITFALLS
- The mixing of the PDMS should be done in many strokes (typically for a few minutes) and preferably in plastic dishes with lids.
- Because of variations between batches, the 50:1 ratio of the Sylgard kit might need adjustment.
- The first bake of the PDMS layer should be fine tuned: too much baking before putting the mold will result in a poor pattern, whereas insufficient baking will result in difficulties separating the mold from the PDMS. Baking times can be reduced by increasing the temperature.
- Before dicing the patterned wafer, make sure the scriber is good by practicing on a similar unpatterned wafer.
- The choice of the cells to use is important: immortalized cell lines often exert forces that are below the force resolution of this method.
- Focal adhesions formed on PDMS may differ, at the molecular level, from those formed on other substrates and their composition (e.g., type of integrin) should be examined.
Acknowledgments
BG is the E. Neter Prof. for cell and tumor biology.
NQB is supported by the Bikura program of the Israel Science foundation and is a fellow of the Center for Complexity; The Horowitz Foundation.
References
Balaban, N. Q., Schwarz, U. S., et al. (2001). Force and focal adhesion assembly: A close relationship studied using elastic micropatterned substrates. Nature Cell Biol. 3(5), 466-472.
Beningo, K. A., and Wang, Y. L. (2002). Flexible substrata for the detection of cellular traction forces. Trends Cell Biol. 12(2), 79-84.
Feynman, R. P. (1964). The Feynman Lecture on Physics. Addison & Wesley.
Galbraith, C. G., Yamada, K. M., et al. (2002). The relationship between force and focal complex development. J. Cell Biol. 159(4), 695-705.
Geiger, B., and Bershadsky, A. (2001). Assembly and mechanosensory function of focal contacts. Curr. Opin. Cell Biol. 13(5), 584-592.
Geiger, B., Bershadsky, A., et al. (2001). Transmembrane crosstalk between the extracellular matrix-cytoskeleton crosstalk. Nature Rev. Mol. Cell Biol. 2(11), 793-805.
Landau, L. D., and Lifshitz, E. M. (1970). "Theory of Elasticity." Pergamon Press, Oxford.
Riveline, D., Zamir, E., et al. (2001). Focal contacts as mechanosensors: Externally applied local mechanical force induces growth of focal contacts by an mDial-dependent and ROCK-independent mechanism. J. Cell Biol. 153(6), 1175-1186.
Roy, P., Rajfur, Z., et al. (2002). Microscope-based techniques to study cell adhesion and migration. Nature Cell Biol. 4(4), E91-E96.
Schwarz, U. S., Balaban, N. Q., et al. (2002). Calculation of forces at focal adhesions from elastic substrate data: The effect of localized force and the need for regularization. Biophys. J. 83(3), 1380-1394.
Whitesides, G. M., Ostuni, E., et al. (2001). Soft lithography in biology and biochemistry. Annu. Rev. Biomed. Eng. 3, 335-373.
Zamir, E., Katz, B. Z., et al. (1999). Molecular diversity of cell-matrix adhesions. J. Cell Sci. 112(Pt. 11), 1655-1669.




